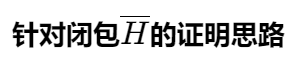
关于
的解释：
拓扑空间与映射连续性的基础概念
关于
这句话的解释：
正规子群的定义：
历史上，伽罗瓦为解决五次以上方程的根的问题，提出了 “置换群” 的概念。他在研究置换群时，发现左陪集等于右陪集的情况（即现在的正规子群），并利用根的置换群的正规子群以及由其确定的商群的思想，成功证明了多项式方程的可解性问题。这一理论成果凸显了正规子群的重要性，也促使数学家们正式定义并深入研究正规子群 。
定义正规子群概念的用处很多，比如
建立群同态与群结构的联系：群同态基本定理建立在正规子群的基础上。在群同态中，任何同态的核都是正规子群；反之，每个正规子群都能对应构造出一个同态。这使得正规子群成为连接群同态与群结构的桥梁，通过对正规子群的研究，能够深入理解群同态的性质和群之间的映射关系，进而分析群的结构和分类 。解决实际问题的需要：在数学的其他分支以及物理、工程等领域，很多实际问题可以抽象为群的问题进行研究，正规子群的引入有助于解决这些实际问题。例如，在物理学的规范场论中，规范群常为连通拓扑群，其正规子群可用于研究规范场在局部区域的行为，从而理解整个物理系统的对称性和相互作用；在机器人运动规划中，可将机器人的运动用拓扑群描述，正规子群的相关理论能帮助处理运动约束和路径规划问题 。
