比如,假设二维向量空间的基(1,0)和(0,1),对偶空间的线性函数φ1(1,0)=2,φ1(0,1)=3和
φ2(1,0)=4,φ2(0,1)=5,以φ1和φ2为基,即函数2x+3y和4x+5y为基构成的空间就是对偶空间:



这里的对偶理论是指,对于向量x=x1α1+x2α2+x3α3+.......,既可以看作是以α1,α2,α3......为基的向量,也可以看作是以x1,x2,x3为基的向量,前提是α1,α2,α3也是线性函数。




这里v是切空间的向量,而dxi是余切空间的向量,dxi(v)可以理解为将向量v在余切空间中线性展开,v(xi)则是将余切向量dx1,dx2,dx3,.....在切空间中展开。
这是因为φ(x1,x2,x3,.....)求导以后得到的微分dx1,dx2,dx3,......满足线性运算的要求,所以得到了余切向量的结论。
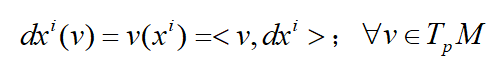


对比切空间向量的展开,切向量是向量,是以偏导数为坐标;而余切空间是由对偶空间的函数组成,是以函数为基向量,所以余切空间是按照函数的全微分进行展开。