研究背景
超导性源于电子对(库珀对)的凝聚,其特征是复杂的序参数,包括振幅和明确的相位。在显微镜下,序参数(Δ)的振幅与库珀配对的强度有关,而超流体刚度(ρs)则表征了凝聚序参数的相位刚度。测量ρs非常重要,因为它不仅是超导态的一个决定性属性,负责零电阻和迈斯纳效应,还能帮助区分常规和非常规超导体。ρs对温度和超流体速度的依赖性具有超导配对对称性的独特特征。例如,铜酸盐中ρs随温度线性变化,表明其超导序参数中存在节点,这是由铜酸盐的非传统d波配对引起的。ρs的大小和掺杂相关性也为超导能隙和电子带结构提供了深入的见解。值得注意的是,在许多非常规超导体中,ρs比传统BCS型超导体小几个数量级,并且遵循与超导相变温度(Tc)相关的异常标度定律。
最近发现的魔角扭曲多层石墨烯(MATMG)为研究强关联电子引起的超导性提供了独特的机会。然而,目前的研究主要依赖于电输运和扫描隧道光谱测量,对超导相的理解仍不完善。电输运实验表明了向列性、泡利极限违反、超导临界电流的异常行为以及与超导态对称破缺的相关性,这表明了BCS物理学之外的范畴。然而,超导态的零电阻限制了通过电输运探索超导圆顶内部结构的可能性。相比之下,扫描隧道光谱研究显示,V形微分电导光谱与节点超导性一致。然而,由于难以区分超导间隙和非超导有序(如风味极化相关态)引起的间隙,这种单粒子隧穿解释变得复杂。因此,需要通过测量热力学量(如ρs)来更好地理解MATMG中的超导序参数。测量ρs可以揭示超导圆顶内部的掺杂演化,并为超导起源提供重要见解。然而,由于样本尺寸和维度的减小,这在技术上具有挑战性。目前,只有基于临界电流密度分析的ρs间接估计可用。
研究成果
近日,哈佛大学Philip Kim和BBN科技公司Kin Chung Fong合作报道了魔角扭曲三层石墨烯(TTG)中ρs的测量,揭示了非常规的节点间隙超导性。利用射频反射技术测量耦合到微波谐振腔的超导TTG的动力学电感响应,发现ρs在低温下呈现线性温度相关性,电流偏置相关性中具有非线性迈斯纳效应,两者都表明了超导序参数中的节点结构。此外,掺杂相关性显示出零温度ρs和超导转变温度Tc之间存在线性关系,这与铜酸盐中Uemura关系类似,表明相位相干限制超导电性。这项研究结果为TTG中的节点超导性提供了有力证据,并对这些石墨烯基超导体的机制提出了重要约束。
相关研究工作以“Superfluid stiffness of twisted trilayer graphene superconductors”为题发表在国际顶级期刊《Nature》上。

研究内容
研究者使用射频(RF)谐振电路来测量微米级扭曲三层石墨烯(TTG)超导体的超流体响应。超导体在有限温度下的微波响应可以用双流体模型来描述,该模型由两个并联通道组成:由凝聚态库珀对组成的超流体通道和由准粒子激发组成的正常流体通道。该模型中与频率(f)相关的复射频电导率包括耗散实部σ1=nne2τn/me和无耗散虚部σ2=nse2/2πfme,其中e和me分别是电子电荷和质量,nn和ns是正常和超流电子密度,τn是准粒子激发的散射时间。
对于频率范围f<fc=(ns/nn)/2πτn,σ1≪σ2,其中fc是截止频率。在这种情况下,超导样品的阻抗主要由特征电感LK=1/(2πfσ2)的无耗散电感通道主导,通常称为动电感。LK与超流体刚度的关系为ρs=(l/w)(1/LK)(单位为H-1)或ρs=(l/w)(ħ2/4e2kBLK)(单位为K),其中w和l分别是器件宽度(垂直于电流)和长度,ħ是普朗克常数,kB是玻尔兹曼常数。因此,通过将超导TTG样品耦合到阻抗匹配的微波谐振器(图1a),谐振频率fr随LK的变化呈线性变化,可以测量TTG样品的超流体刚度。

图1. 实验装置和设备表征

图2. 温度和掺杂相关的超流体刚度
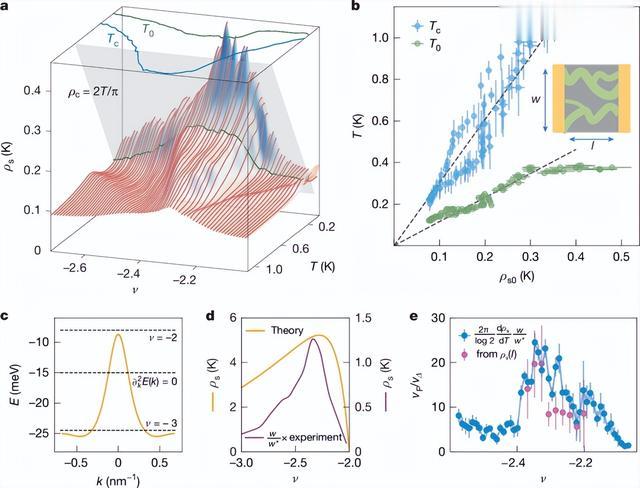
图3. BKT跃迁、Uemura关系和节点配对对称性

图4. 非线性迈斯纳效应
结论与展望
这项研究的超流体刚度测量对MATMG超导性质提供了重要见解。测量结果显示,超流体刚度随温度线性下降,同时观察到非线性迈斯纳效应及其温度相关性,这些特征的融合为节点配对对称性提供了强有力的证据。此外,零温度极限下的超流体刚度与超导转变温度之间的线性关系表明,超导转变是由相位波动而非库珀对断裂所控制,这是一种非常规现象。
